Geometric algebra

Related: Clifford algebra.

An Intuitive Introduction

For a more in-depth explanation, you can refer to "What is Geometric Algebra?" in the Calibre Library. In a nutshell, the exterior algebra can be constructed for any vector space $V$, using $V$ itself rather than its dual $V^*$. This results in a graded algebra:

The elements of this algebra can be interpreted as scalars, vectors, bivectors, trivectors, etc. A bivector $u \wedge v$ can be understood as the plane spanned by $u, v$ along with the area of the parallelogram and the orientation from $u$ to $v$. Similar interpretations can be made for a $k$-vector.

In the algebra $\Lambda(V)$, we have operations like addition, scalar multiplication, inner product for vectors, and wedge product for any $k$-vectors. All of these can be generalized by a new operation known as the geometric product. For vectors, it takes the following form:

Geometric Algebra in 2D and Complex Numbers

When we set $V = \mathbb{R}^2$, it can be shown that $G^2 = \Lambda(\mathbb{R}^2)$ naturally contains complex numbers. Given a basis $\{ e_1, e_2 \}$, we have:

Therefore, we interpret $e_1 e_2$ as $i$. Furthermore, it can be shown that:

• $\mathbb{R} \oplus \Lambda^2(\mathbb{R}^2)$ is isomorphic to $\mathbb{C}$, with its usual internal rotations.

• $\mathbb{R} \oplus \Lambda^2(\mathbb{R}^2)$ acts on $\Lambda^1(\mathbb{R}^2) = \mathbb{R}^2$ as dilation-rotations. Specifically, the exponent $e^{I \theta}$ rotates a vector $a \in \mathbb{R}^2$ by $2\theta$ through the formula $a' = e^{-I \theta} a e^{I \theta}$.

Note: Although $e^{I \theta}$ acts on $\Lambda^1(\mathbb{R}^2)$ to produce a rotation of $\theta$, which seems natural, this behavior is not generalizable to all dimensions.

Complex number has a doubled "personality": they represent vectors and operations on vectors. On the other hand, the real and imaginary part of a product of complex number has no geometric meaning. From the Geometric Algebra view, everything is more coherent. The geometric algebra that start with $\mathbb{R}^2$, say $\mathcal{G}^2$, provide us with:

• The real plane $\mathbb{R}^2$ itself, that is, its grade 1 members.

• An even subalgebra $\mathbb{R} \oplus \mathcal{G}^2_2$ that operates over $\mathbb{R}^2$ in the sandwiched way.

The geometric product on this even subalgebra is similar to the complex product. And moreover, acts over $\mathbb{R}^2$ in the expected way: rotation-dilation. But we have two unexpected issues:

• The action is not only by multiplication, but on the sandwich way...

• We have an identification of $\mathcal{G}_1 ^2$ with $\mathbb{R} \oplus \mathcal{G}_2 ^2$ via $v\mapsto e_1 v$. The geometric product at $\mathcal{G}_1 ^2$ yields an element of $\mathbb{R} \oplus \mathcal{G}_2 ^2$ that can be returned back to $\mathcal{G}_1 ^2$, giving rise to a vector product that is not the usual complex product. On the contrary, it corresponds to

With this product, both real and imaginary part has geometric meaning: the cosine of the angle and the area of the parallelogram.

Geometric Algebra in 3D and Quaternions

When we take $V = \mathbb{R}^3$, $G^3 = \Lambda(\mathbb{R}^3)$ contains quaternions $\mathbb{H}$ in a natural way. With a fixed basis $\{ e_1, e_2, e_3 \}$, it turns out that $e_2 e_3, e_1 e_3, e_1 e_3$ behave like the imaginary units $i, j, k$ in $\mathbb{H}$. Therefore:

• $\Lambda^2(\mathbb{R}^3)$ are the pure imaginary quaternions.

• $\mathbb{R} \oplus \Lambda^2(\mathbb{R}^3)$ is isomorphic to $\mathbb{H}$, maintaining its usual internal properties.

• An unitary vector $a \in \mathbb{R}^3$ defines a reflection in $\mathbb{R}^3$ along the plane orthogonal to it through the formula $x' = -a x a$.

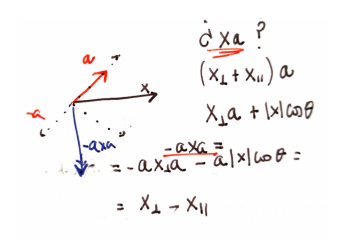
• $\mathbb{R} \oplus \Lambda^2(\mathbb{R}^3)$ acts on $\Lambda^1(\mathbb{R}^3) = \mathbb{R}^3$ as rotations. Specifically, the exponent $e^{B \theta}$ rotates a vector $a \in \mathbb{R}^3$ by $2\theta$ along the plane given by $B$ using the formula $e^{-B \theta} a e^{B \theta}$.

Axiomatic approach

We can invert the entire construction process to define a geometric algebra as follows:

Definition:

A geometric algebra is a set $\mathcal{G}$ equipped with two composition laws—addition and multiplication (referred to as the *geometric product*)—that meet the following criteria:

1. $\mathcal{G}$ is a (potentially non-commutative) graded ring with a unit element. The neutral elements for addition and multiplication are denoted by 0 and 1, respectively.

2. The grade-0 elements, $\mathcal{G}_0$, constitute a field with characteristic 0 that includes the neutral elements 0 and 1. The elements of $\mathcal{G}_0$ commute under multiplication with any element in $\mathcal{G}$, meaning they are contained in the *center* of $\mathcal{G}$. Hence, $\mathcal{G}$ can be viewed as an associative algebra over $\mathcal{G}_0$.

• Elements of $\mathcal{G}_0$ are called scalars or 0-vectors.

3. $\mathcal{G}$ includes a subset $\mathcal{G}_1$ that is closed under addition, and its elements are termed 1-vectors.

• The square of a 1-vector is a scalar, and if $a \neq 0$,

• $$

4. For $\mathbf{a} \in \mathcal{G}_1$ and $\mathbf{A}_k \in \mathcal{G}_k$, we can define the inner product as

• $$

• and the outer product as

• $$

• Consequently,

• $$

• We assume that:

• - $a \cdot A_k \in \mathcal{G}_{k-1}$

• - $a \wedge A_k \in \mathcal{G}_{k+1}$

5. There exists a certain $n \in \mathbb{N}$ such that for every $A_n \in \mathcal{G}_n$,

and

for $j = 0, 1, \ldots, n$.

Some remarks:

• The neutral $0 \in \mathcal{G}_0$ (as a scalar) is identical to $0 \in \mathcal{G}_1$ (as a 1-vector).

• The first part of axiom 3 is equivalent to: *for any $u, v \in \mathcal{G}_1, u \cdot v \in \mathcal{G}_0$*. Thus, it can be deduced from axiom 4.

• Elements of $\mathcal{G}_r$ are known as $r$-vectors. If an element contains only one term, it is called a simple $r$-vector or $r$-blade. In general, a geometric product of $r$ vectors (which are not necessarily orthogonal) is termed an $r$-versor.

• If $\mathcal{G}_1$ has dimension 3, then one can show that the linear combination of 2-blades can always be reduced to a single 2-blade (for instance, in $\mathbb{R}^3$, two planes always share a common line). However, this does not hold in higher dimensions.

• Concerning axiom 2, every ring $R$ (even a non-commutative one) can be viewed as an associative algebra over its center. Conversely, if $R$ is an associative algebra over a commutative subring $S$, then $S$ is a subset of the center of $R$.

• Within the list of axioms, we have incompletely defined two products. Several properties can be shown about these products that one would intuitively expect, such as the associativity of the wedge product and the distributive rules for both the inner and wedge products.

• The definitions of the inner and wedge products within the axioms can and should be generalized to any pair $A_r, B_s$ of multivectors:

• $$

• and

• $$

• where $\langle \quad \rangle_j$ signifies projection over $\mathcal{G}_j$.

• To understand the significance of $a \cdot B$, let $B = b \wedge c$. Following the definitions, we find:

• $$

• Manipulating this equation leads to:

• $$

• This expression shows that $a \cdot (b \wedge c)$ is a vector contained in the plane spanned by $b$ and $c$ and is orthogonal to the projection of $a$ onto that plane.

• Two vectors are orthogonal if $u \cdot v = 0$. This implies $u v = u \wedge v$, and vice versa. For three orthogonal vectors $\{ e_i \}$, $e_i \cdot e_j = 0$ implies:

• $$

• Another useful definition is that of reversion. It is the unique operation in $\mathcal{G}$ satisfying:

• $$

• This implies:

• $$

• Yet another definition is magnitude. For any multivector $A \in \mathcal{G}$:

• $$

• Finally, a rotor is defined as a geometric product of an even number of unit vectors such that $R^{-1} = R^{\dagger}$.

Geometric interpretations

(see anotacioneslatex.tex)

Angles and trigonometry

(see anotacioneslatex.tex)

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es